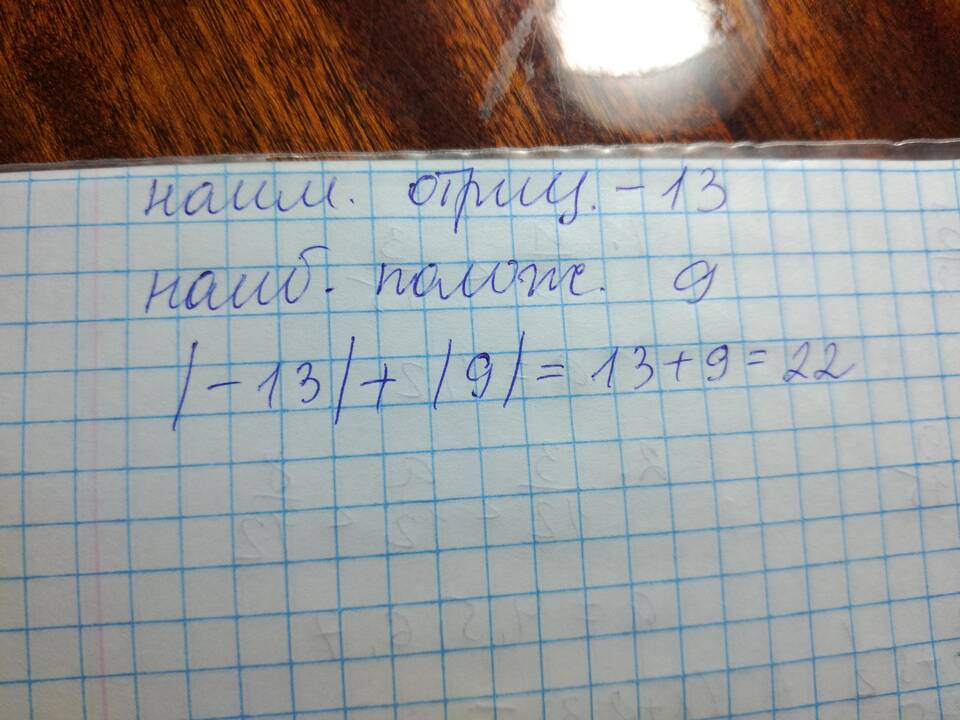Модуль числа - это его абсолютное значение без учета знака. Рассмотрим методы вычисления суммы модулей для различных наборов чисел.
Содержание
Основные понятия
- Модуль положительного числа равен самому числу
- Модуль отрицательного числа равен ему с противоположным знаком
- Модуль нуля равен нулю
- Сумма модулей всегда неотрицательна
Формула вычисления модуля
Для любого действительного числа a:
|a| = a, если a ≥ 0
|a| = -a, если a < 0
Примеры вычисления суммы модулей
| Числа | Вычисление | Результат |
| 5, -3, 2 | |5| + |-3| + |2| = 5 + 3 + 2 | 10 |
| -7, -4, 0 | |-7| + |-4| + |0| = 7 + 4 + 0 | 11 |
Вычисление суммы модулей в программировании
На языке Python
- Использование функции abs() для каждого числа
- Суммирование результатов:
numbers = [5, -3, 2]
sum_of_abs = sum(abs(x) for x in numbers)
Свойства суммы модулей
- Неравенство треугольника: |a + b| ≤ |a| + |b|
- Сумма модулей всегда ≥ модуля суммы
- Коммутативность: порядок слагаемых не влияет на результат
- Ассоциативность: группировка слагаемых не влияет на результат
Геометрическая интерпретация
- На числовой прямой модуль - расстояние от точки до нуля
- Сумма модулей - сумма таких расстояний
- Для комплексных чисел - аналогично в комплексной плоскости
Применение суммы модулей
| Область | Применение |
| Статистика | Вычисление среднего абсолютного отклонения |
| Физика | Расчет суммарных величин, где направление не важно |
| Экономика | Анализ абсолютных изменений показателей |
Вычисление суммы модулей - базовая математическая операция, имеющая широкое применение в различных областях науки и практической деятельности.