Сумма единиц - это математическое понятие, которое может рассматриваться в разных контекстах. Рассмотрим основные трактовки этого выражения.
Содержание
Сумма единиц - это математическое понятие, которое может рассматриваться в разных контекстах. Рассмотрим основные трактовки этого выражения.
Арифметическая сумма единиц
В простейшем случае сумма единиц представляет собой результат сложения числа 1 несколько раз:
| Количество единиц | Сумма |
| 1 | 1 |
| 2 | 2 |
| 5 | 5 |
| n | n |
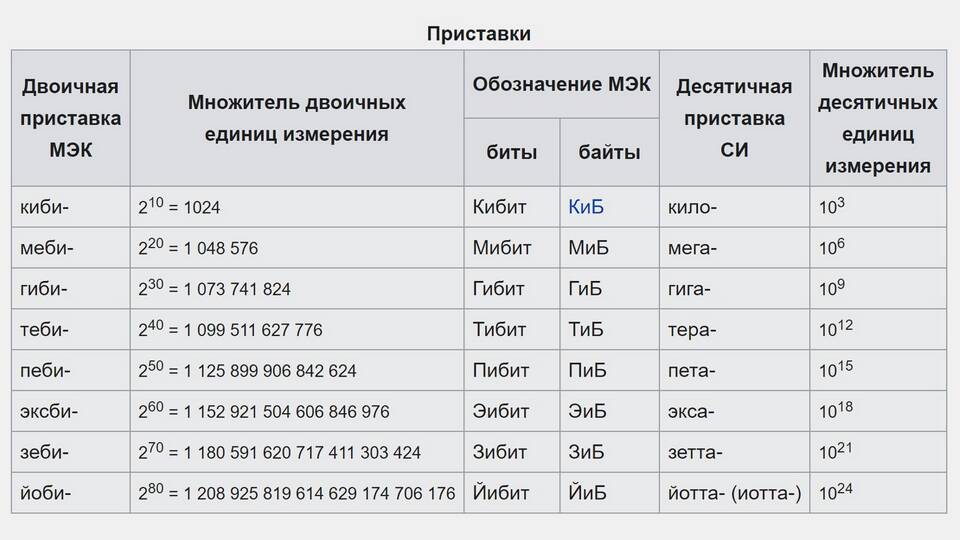
Сумма единиц в двоичной системе
В двоичной системе счисления сумма единиц имеет особое значение:
- 1 + 1 = 10 (в двоичной системе)
- 1 + 1 + 1 = 11
- Сумма n единиц дает число, состоящее из n единиц в двоичной записи
Сумма единиц в алгебре
В алгебраических выражениях сумма единиц может принимать различные формы:
- ∑(1) от k=1 до n = n
- 1 + 1 = 2 (в поле действительных чисел)
- 1 + 1 = 0 (в поле характеристики 2)
Примеры в разных алгебраических структурах
| Структура | Результат 1+1 |
| Натуральные числа | 2 |
| Булева алгебра | 1 |
| Z₂ (по модулю 2) | 0 |
Геометрическая интерпретация
В геометрии сумму единиц можно представить как:
- Сложение единичных векторов
- Объединение единичных отрезков
- Сложение площадей единичных квадратов
Философский аспект
В философии математики сумма единиц рассматривается как:
- Проблема определения базовой единицы
- Вопрос о природе сложения
- Проблема тождества и различия
Таким образом, сумма единиц - фундаментальное понятие, которое в разных разделах математики и смежных дисциплинах может иметь различные значения и интерпретации.
